¿Existe el Azar?

Lorelei Ambriz
Technician

Una breve e informal introducción a la teoría del caos matemático y la teoría de la probabilidad matemática.
Para poder responder a la pregunta sobre la existencia del azar, primero abordaremos otro concepto con el cual posiblemente ya estemos parcialmente familiarizados. Dicho concepto es el caos matemático, o también conocido coloquialmente como el efecto mariposa. Así como algunos conceptos relacionados a este: sistemas dinámicos y determinismo.
¿Qué es el caos matemático?
En resumen, la teoría del caos, o caos matemático (para no perder de vista las matemáticas) tiene como centro de estudio, los sistemas dinámicos que aparentan tener un comportamiento aleatorio, sin embargo estos son gobernados por patrones y determinismo.
¿Qué es un sistema dinámico?
Un sistema dinámico es un conjunto de fenómenos deterministas que interactúan uno con otro dentro de este conjunto en función de una colección de parámetros (usualmente el parámetro más usado es el tiempo).
Un ejemplo sencillo de sistema dinámico es un péndulo simple. Para detallar un poco más, mencionemos los componentes de este sistema. Un péndulo simple consiste en un tubo/varilla que en uno de los extremos sostiene un peso mientras que del otro, estará sostenido de forma que pueda columpiarse. Los componentes de este sistema son: la longitud de la varilla, el peso que carga, la fuerza gravitatoria y la altura inicial a la que hará su primera oscilación. El resultado de la ejecución de este sistema es una medición del tiempo.
Un ejemplo mucho más sofisticado es el planeta Tierra. Entre sus componentes más notorios están: árboles, agua, aire, radiación recibida por el sol, la geografía del planeta, etc. Uno de los resultados apreciables en este sistema como resultado de estos componentes es el clima de la Tierra.
¿Qué es el determinismo?
Decimos que un modelo es determinista cuando existe una ley o regla que siempre va a cumplir dicho modelo asociado a un fenómeno particular. O en otras palabras, está determinado por dichas leyes y las condiciones que le rodean. Por dar un ejemplo, como si se tratase de la descripción de la maquinaria en un reloj con péndulo. En esta maquinaria hay todo un sistema dinámico que cambia con respecto al tiempo. Poseé un conjunto de engranajes, manecillas y un péndulo, que organizados de forma específica, nos dará como resultado un dispositivo con el que medir el tiempo a lo largo de un día.
Para comprender y/o descubrir las leyes o reglas que gobiernan estos sistemas, los matemáticos, en resumen, recurrimos a la búsqueda de patrones con un razonamiento lógico deductivo así como algunas veces es necesaria la experimentación e incluso el método científico.
Y ahora, ¿Qué sigue?
Habiendo hablado un poco sobre sistemas dinámicos, determinismo y caos matemático introduciremos el siguiente concepto: estabilidad de sistemas dinámicos. ¿Cómo podemos considerar la estabilidad?. Sin entrar en el rigor matemático pero con algo de matemáticas, un sistema es estable cuando tenemos una curva ‘f’ definida por una condición inicial ‘x0’ en este sistema y trazamos una “tubería” alrededor de esta curva para que quede contenida en esta (vecindad de convergencia). Y entonces para cualquier condición inicial ‘t0’ cercana a ‘x0’, que nos define una curva ‘g’ ocurrirá uno de los siguientes casos:
- Si g → f (tiende o cada vez se acerca más a f) entonces el sistema es asintóticamente estable.
- Si g permanece dentro de la tubería en todo momento, entonces el sistema es estable.
- Si a partir de un momento, g sale de la tubería y de cualquier tubería con centro en f, entonces el sistema es inestable.
Observación: si ‘g’ saliera 1 vez (o incluso n veces), entonces hacemos una tubería con centro en f que contenga a toda la curva g. Por eso se dice que sale de todas las tuberías posibles, porque entonces ‘g’ se vuelve completamente diferente a ‘f’ a partir de algún momento.
Ahora usando ejemplos con pares idénticos de péndulos para tener una mayor visibilidad de los casos anteriores:
- Levanta el par de péndulos, y al soltarlos de forma simultánea, estos oscilarán con la misma frecuencia y se detendrán casi al mismo tiempo. Esto es estabilidad asintótica.
- Levanta el par de péndulos, pero instalados sobre una “máquina de movimiento perpetuo”. Al soltarlos estos oscilarán con la misma frecuencia hasta que se detenga la máquina.
- Ahora considera un par de péndulos dobles, y levanta dicho par a una misma posición. Al soltar los péndulos, después de unos segundos cada péndulo tendrá su trayectoria completamente diferente al otro. Esto es inestabilidad. De hecho, en este caso en particular, las trayectorias parecieran ser aleatorias. Sin embargo siguen cumpliendo las leyes que rigen a los péndulos.
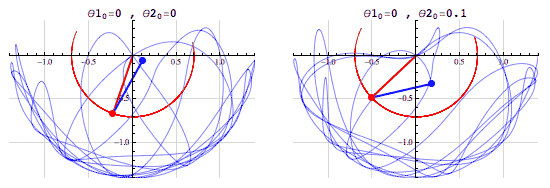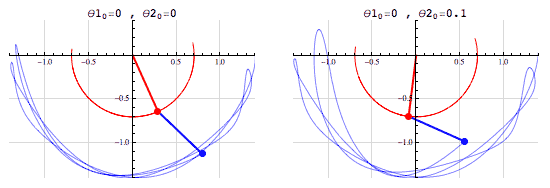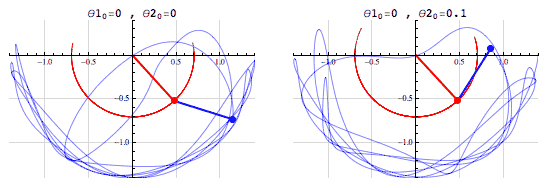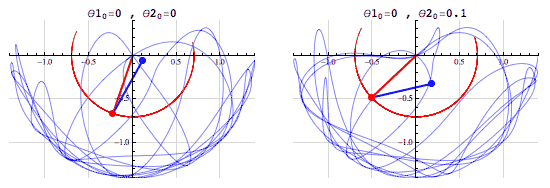
Cabe recordar que aunque creamos ponemos a la misma altura los péndulos, en el mundo físico hay una diferencia mínima entre estas alturas. Para los sistemas estables, la estabilidad parece menospreciar dicha diferencia. En cambio, el sistema inestable es altamente sensible a estos cambios y esta pequeña diferencia inicial termina siendo una enorme diferencia al poco tiempo.
¿Dónde más podemos ver el caos matemático?
La respuesta es relativamente fácil: en casi todos los lugares a donde miremos. Desde las trayectorias y posición donde caen las hojas de un árbol al desprenderse de sus ramas, las acciones de las acciones en la bolsa, hasta incluso los procesos biológicos de los seres vivos y sin olvidar un ejemplo muy importante: el clima de la Tierra. Una persona podría reflexionar que todo el universo está gobernado por caos matemático, determinismo absoluto. Simplemente las relaciones que ocurren entre los componentes del universo pueden ser desde relativamente simples, a altamente complejas.
Ahora con todo lo planteado: ¿Existe el azar?
La respuesta pareciera ser que no. Sin embargo, notemos un detalle importante sobre lo que conocemos del azar: podemos tener la seguridad que un resultado o salida obtenido de un evento aleatorio es desconocido, ya que si lo supiéramos de antemano, entonces el evento no sería aleatorio. En este punto pareciera que podemos ver el caos matemático como azar, sin embargo este es determinista y eso nos implica que conociendo todos los componentes que definen esta curva (leyes, condiciones iniciales e interacciones entre todas las variables), podemos conocer de antemano todas las salidas. Pero aquí está precisamente el detalle: conocer todas las interacciones de forma precisa entre todas las variables. Cuando estas interacciones se vuelven muy complejas dentro del sistema y este se vuelve inestable, en lugar de intentar comprender lo que ocurre entre estas variables, podemos empezar a analizar las posibles salidas o resultados de este. De este análisis podemos ver que otros patrones empiezan a emerger: distribuciones de probabilidad.
Distribuciones de probabilidad: un vistazo a la teoría de la probabilidad.
La teoría de la probabilidad es una rama dentro de las matemáticas que estudia los eventos aleatorios y estocásticos. Si bien la teoría clásica de la probabilidad se reduce a hacer conteos de casos favorables y compararlos contra todos los posibles escenarios, cuando se propone un conjunto de axiomas basados en la teoría de conjuntos y la teoría de la medida por parte de Andréi Kolmogórov es que la teoría de la probabilidad adquiere rigor matemático y así se puede extender su estudio más allá de los marcos clásicos de esta. Argumentos en el contexto de la probabilidad utilizados en diversas áreas como la física, economía, biología entre otras cobran fuerza gracias a esta aportación. A partir de aquí es que surge la teoría moderna de la probabilidad. Algunos de los conceptos y resultados más importantes de esta teoría moderna son:
- Variables aleatorias y funciones de distribución.
- Leyes de los grandes números.
- Teorema del límite central.
- Procesos estocásticos.
Conexión entre los sistemas caóticos y la probabilidad.
Como platicamos anteriormente, estudiando las salidas o resultados de sistemas dinámicos inestables podemos ver que hay patrones que emergen de estos. Curiosamente estos se comportan como variables aleatorias y funciones de distribución de la teoría de la probabilidad. Esto se debe a algunos resultados importantes como son las leyes de los grandes números y el teorema del límite central entre otros. Recordando que la teoría de la probabilidad adquiere su rigurosidad a partir de los axiomas de Kolmogorov que tienen origen en la teoría de conjuntos y la teoría de la medida.
Entonces: ¿el azar existe?
Si bien podemos concluir que el universo es gobernado por leyes de las cuales algunas conocemos y otras no (de aquí podemos abrir otro tema para otra ocasión: Lo que sabemos, lo que no sabemos, y lo que no sabemos que no sabemos), y esto tiene implícito la omnipresencia del determinismo. Podemos concluir que el azar no tiene lugar en el universo. Sin embargo, recordemos que la teoría de la probabilidad es una construcción humana, cuya rigurosidad y patrones pueden ser conectados con otras áreas, y como ya vimos, particularmente pueden ser conectados con el caos matemático para cambiar el enfoque de estudio de los fenómenos regidos por el caos. Pasando de conocer las leyes que los gobiernan para entender las salidas y resultados de estos, a conectar dichos patrones con las distribuciones de probabilidad que tienen toda una teoría matemática que las respalda, así como un área que las explota como es la estadística.
Explotando el azar
Sabiendo que el azar está directamente conectado con el desconocimiento de resultados y ocurrencias. Y precisamente por esta razón es que podemos explotar la teoría de la probabilidad, entonces podemos pasar a construir un objeto muy importante dentro de la ciencia de la computación: los generadores de números aleatorios.
Estos generadores son objetos muy útiles para dotar de nuestros procesos con la esencia del caos y así traer la complejidad del mundo a nuestros análisis, modelos, simulaciones y demás. Sin embargo, cabe mencionar que para obtener generadores de números aleatorios que en verdad tengan lo que buscamos, es importante notar que no debe haber un patrón sencillo en estos. ¿Entonces cómo podemos recurrir a construir un buen generador de números aleatorios?. La respuesta se encuentra en el mismo caos. Por ejemplo, usar las curvas que recorren los péndulos dobles, o la paridad en los dígitos decimales de π, entre otros.
Simulando el azar en nuestros procesos, podemos aprovechar una de las características más importantes de este, la cual es: la imparcialidad. Con esta, eliminamos sesgos de nuestras muestras (característica fundamental para entrenar con imparcialidad a nuestros modelos de aprendizaje máquina), contribuyendo incluso al mismo entrenamiento que ocurre en los modelos de aprendizaje máquina y aprendizaje profundo por medio de la optimización de las funciones de costo. Otra simulación muy importante a mencionar es la simulación de MonteCarlo, la cuál nos permite obtener muestras aleatorias que representan lo que podemos modelar, así como pueden ser usadas para diferentes cálculos computacionales pesados que de forma clásica podrían ser desde muy complejos, hasta imposibles.
Conclusión
El azar es un constructo humano que si bien no existe en el universo de forma natural debido a la naturaleza compleja de este, como concepto humano nos ayuda a comprender y estudiar lo que sucede reduciendo la complejidad que surge de forma natural. Así que en efecto, el azar existe, porque la humanidad lo construyó y un día se dió cuenta que le ayudaba a comprender mejor el complejo universo en el que vivimos.